Πυθαγόρας ο Σάμιος, η προσφορά του στα μαθηματικά, στη μουσική, στη γεωμετρία και στην αστρονομία

Σύνταξη άρθρου: Τάσσος Κυρίκος, Λέντια Ρουστέμι

Επιμέλεια άρθρου: Κωνσταντίνος Ουρανός

 

Τα λογικά όντα διακρίνονται σε θεούς, σε ανθρώπους και σε πλάσματα όπως ο Πυθαγόρας

                                                                                                      ΑΡΙΣΤΟΤΕΛΗΣ

Η ζωή του

Η πρώτη ολοκληρωμένη βιογραφία του Πυθαγόρα είναι του Διογένη του Λαέρτιου στο όγδοο βιβλίο των Βίων των Φιλοσόφων. Υπάρχουν και άλλες μεταγενέστερες βιογραφίες, όπως αυτή του Πορφύριου «Πυθαγόρου Βίος» και του Ιάμβλιχου «Περί του Πυθαγορικού Βίου».

Ο Πυθαγόρας γεννήθηκε στη Σάμο μεταξύ του 580 και του 570 π.Χ. . Ο πατέρας του ήταν ο Μνήσαρχος (ή Μνήμαρχος) χαράκτης δακτυλιολίθων και μητέρα του η Πυθαΐδα (ή Παρθενίδα), η πιο ωραία Σαμιώτισσα.

Οι δακτυλιόλιθοι είναι δαχτυλίδια που έχουν έναν σφραγιδόλιθο, πάνω στον οποίο είναι χαραγμένο ένα σύμβολο, το οικόσημο της οικογένειας ή του βασιλικού οίκου.

Ο πατέρας του λέγεται ότι είχε ζητήσει χρησμό στο μαντείο των Δελφών για ένα ταξίδι του στη Συρία. Η Πυθία προφήτευσε μεγάλο κέρδος από το ταξίδι του και ότι θα αποκτήσει παιδί, που θα διαφέρει σε ομορφιά και σοφία από τους άλλους ανθρώπους και θα ωφελήσει το ανθρώπινο γένος σε όλη τη ζωή του. Επειδή η γέννηση του γιου του προφητεύτηκε από τον Πύθιο Απόλλωνα, ο Μνήμαρχος ονόμασε το παιδί του Πυθαγόρα. Λόγω της ευγενικής του καταγωγής, ένας Σάμιος ποιητής ισχυρίστηκε ότι ο Πυθαγόρας είναι γιος του Απόλλωνα, λέγοντας ότι:

«Τον Πυθαγόρα, τον αγαπητό στον Δία, τον γέννησε με τον Απόλλωνα η Πυθαΐδα, η πιο όμορφη Σαμιώτισσα».

Ο Πυθαγόρας παντρεύτηκε τη Θεανώ, κόρη του Πυθώνακτα, με την οποία απέκτησε τέσσερα παιδιά, τον Τηλαύγη, τη Δαμώ, τη Μυία και την Αριγνώτη, που όλα έγιναν σημαντικοί φιλόσοφοι. Η Μυία, σύμφωνα με τον Τίμαιο, όταν μεγάλωσε έγινε αρχηγός των γυναικών της πόλης του Κρότωνα.

Τα ταξίδια του Πυθαγόρα

Στην ηλικία των δεκαοκτώ ετών εγκατέλειψε τη Σάμο, λόγω του τυραννικού καθεστώτος του Πολυκράτη.

Περιόδευσε στη Μικρά Ασία, όπου στη Μίλητο από τον Θαλή, διδάχθηκε Μαθηματικά και πώς θα αξιοποιεί τον χρόνο του, να τρώει υγιεινά, να αποφεύγει το κρασί και το κρέας, να κοιμάται λίγο, να έχει σωματική υγεία, να είναι σε διαρκή εγρήγορση και να έχει καθαρή ψυχή.

Μετά ταξίδεψε στη Σιδώνα και μυήθηκε σε όλες τις θείες τελετές που τελούνταν στην Τύρο, τη Βύβλο και στις άλλες πόλεις της Συρίας. Η ενασχόλησή του με τις τελετές αυτές ήταν η μεγάλη επιθυμία του για μάθηση.

Με προτροπή του Θαλή ταξίδεψε στην Αίγυπτο, όπου παρέμεινε είκοσι δύο χρόνια ασχολούμενος με τη Γεωμετρία, την Αστρονομία τη Μουσική και μυούμενος σε όλες τις τελετές των θεών.

Από την Αίγυπτο μεταφέρθηκε αιχμάλωτος από τους στρατιώτες του Καμβύση στη Βαβυλώνα, όπου παρέμεινε για δώδεκα χρόνια. Εκεί ήλθε σε επαφή με τα περσικά μυστήρια και τον Ζωροαστρισμό. Με τη βοήθεια των Μάγων έφθασε στο υψηλότερο σημείο γνώσης των αριθμών, της μουσικής και της αστρονομίας.
Ο Πυθαγόρας επέστρεψε στη Σάμο σε ηλικία πενήντα έξι ετών και ίδρυσε Σχολή.
Εξ αιτίας του τυραννικού καθεστώτος του Πολυκράτη και της αδιαφορίας των Σαμίων για όσα τους δίδασκε έφυγε και πάλι από τη Σάμο.

Ταξίδεψε στη Νότια Ιταλία, τη «Μεγάλη Ελλάδα» στην πόλη του Κρότωνα, που ήταν φημισμένη για τους μαθηματικούς της, τους φυσικούς, τους αθλητές και για τους γιατρούς της. Εκεί στον Κρότωνα ίδρυσε Σχολή στην οποία δίδασκε τις ιδέες του κυρίως στην ανώτερη κοινωνική τάξη.

Λόγω των πολιτικών του απόψεων ήρθε σε ρήξη με τους δημοκρατικούς, οι οποίοι καταδίωξαν τον Πυθαγόρα και τους μαθητές του και έκαψαν τη Σχολή τους. Αυτή τη ρήξη την υποκίνησε ο Κύλων, ένας πλούσιος πολίτης του Κρότωνα, τον οποίο ο Πυθαγόρας δε δέχθηκε στη σχολή του λόγω του χαρακτήρα του.

Ο Πυθαγόρας πέθανε είτε κατά τον εμπρησμό της Σχολής του είτε αργότερα στο Μεταπόντιο σε ηλικία 80 ετών.

 

Η Σχολή των Πυθαγορείων

Η σχολή που ίδρυσε ο Πυθαγόρας στον Κρότωνα, πολύ σύντομα απέκτησε μεγάλη φήμη.

Η διδασκαλία του στηρίχτηκε στη ζωντανή επαφή με τους μαθητές του, τον υποδειγματικό τρόπο ζωής του και στη θέσπιση κανόνων πίστης και συμπεριφοράς που είχαν ως αποτέλεσμα τη συνοχή της κοινότητας.

Στα νέα μέλη της κοινότητας επιβαλλόταν σιωπή κατά την περίοδο της μαθητείας τους, η οποία διαρκούσε πέντε χρόνια. Μετά αποκτούσαν το δικαίωμα των μυημένων και είχαν προσωπική επαφή με τον Πυθαγόρα.

Κάθε μέλος της κοινότητας έπρεπε να αποδεχθεί νόμους και εντολές, που είχαν τεθεί από τον Πυθαγόρα, σαν να ήταν θεϊκές εντολές. Ο ομαδικός τρόπος ζωής στηρίχτηκε στη φιλία, την αλληλεγγύη και στην κοινοκτημοσύνη (διέθεταν τις περιουσίες τους για το κοινό όφελος). Ο Πυθαγόρας δίδασκε τη λατρεία των θεών, το σεβασμό προς όσους έχουν πεθάνει, τη νομοθεσία, την παιδεία, την εχεμύθεια, τη σωφροσύνη, τον σεβασμό της οικογένειας, την εγκράτεια, την απαγόρευση της μοιχείας και τη φροντίδα για τα ζώα.

Ο Πυθαγόρας, σύμφωνα με τον Ιάμβλιχο, είχε διατυπώσει το απόφθεγμα ότι:

«Πρέπει να αποφεύγεται με κάθε τρόπο και να κόβεται δια πυρός και σιδήρου και με οποιονδήποτε τρόπο

• από το σώμα η ασθένεια
• από την ψυχή η αμάθεια
• από την κοιλιά η πολυτέλεια
• από την πόλη η πολιτική εξέγερση
• από την οικογένεια η διχόνοια και
• από όλα η έλλειψη μέτρου».

Από τους μαθητές του επέλεγε εκείνους που είχαν ιδιαίτερες ικανότητες και ενδιαφέροντα και τους μυούσε στα μυστικά της «πυθαγόρειας τάξης». Μυστικιστικό σύμβολο της «πυθαγόρειας τάξης» ήταν η πεντάλφα, δηλαδή ένα αστεροειδές πεντάγωνο.

Στη σχολή του γίνονταν δεκτές και γυναίκες, από τις οποίες μερικές, όπως η Δαμώ, η Θεανώ (σύζυγος του Πυθαγόρα), η Αριγνώτη, η Μελίσσα, η Περικτιόνη (μητέρα του Πλάτωνα), η Αρετή, έγιναν σημαντικοί φιλόσοφοι. Μάλιστα ίδρυσε σύλλογο γυναικών.

Ένα μεγάλο μέρος της πυθαγόρειας θεωρίας ήταν μυστικιστικό αλλά περιείχε και ηθικές δοξασίες και γινόταν πάντοτε μαθηματική θεμελίωση.

Πίστευε ότι η ψυχή είναι αθάνατη και μεταβαίνει σε άλλο σώμα (μετενσάρκωση).

Η μύηση στην Πυθαγόρεια φιλοσοφία είναι διαδικασία κάθαρσης δια της επιστήμης, ώστε η ψυχή να μπορέσει να απελευθερωθεί από τον κύκλο της μετενσάρκωσης, για να φθάσει στη θεότητα από την οποία προέρχεται.

Από τις διδασκαλίες των πυθαγορείων πολλές έχουν χαθεί, γιατί τα μέλη της «πυθαγόρειας τάξης» είχαν ορκισθεί να μην αποκαλύψουν όσα τους δίδασκε ο Πυθαγόρας.

Ο Πυθαγόρειος Αρχύτας ο Ταραντίνος είχε διαιρέσει τα Μαθηματικά στα εξής μέρη:

Μουσική – Αριθμητική – Γεωμετρία – Αστρονομία

Τα μέρη αυτά αποτελούσαν το «τετράδιο». Τα περιεχόμενο των μαθημάτων έγινε αποδεκτό από τον Πλάτωνα και τον Αριστοτέλη και διατηρήθηκε για αιώνες μέχρι την Αναγέννηση ως καθιερωμένη σχολική ύλη.  

 

Μουσική

Σύμφωνα με τον Ρωμαίο Βοήθιο (6^ος αιώνας μ.Χ.), μια ημέρα στην Αλεξάνδρεια, ο Πυθαγόρας περνούσε έξω από το εργαστήριο ενός σιδερά όπου τέσσερις τεχνίτες χτυπούσαν με τα σφυριά τους ένα μέταλλο. Παρατήρησε ότι από τα χτυπήματα των διάφορων σφυριών πάνω στο αμόνι εκπέμπονταν ήχοι, που συνέθεταν μια ωραία μουσική. Μπαίνοντας στο εργαστήριο παρατήρησε ότι το μουσικό αποτέλεσμα οφειλόταν στα σφυριά των οποίων τα βάρη ήταν ανάλογα των αριθμών 12, 9, 8, 6. Συγκρίνοντας, ως προς το βάρος, το πιο βαρύ σφυρί με τα υπόλοιπα βρήκε τους λόγους

αντίστοιχα. Σκέφτηκε ότι οι λόγοι αυτοί να είχαν κάποια σχέση με τους ήχους που άκουσε. Τα μουσικά διαστήματα που άκουσε ήταν η αυτά που λέγονται η τέταρτη, η πέμπτη και η όγδοη αρμονική (η μέτρηση από τον φθόγγο που έδινε το πιο βαρύ σφυρί).

 

Αυτό όμως ίσως είναι ένας μύθος, γιατί το παραγόμενο αποτέλεσμα δεν ταιριάζει με τη σχέση «βάρος σφυριού» και «ύψος ήχου».

Σύμφωνα με τις διηγήσεις του Βοήθιου ο Πυθαγόρας ερεύνησε τη σχέση του μήκους μιας παλλόμενης χορδής και του μουσικού τόνου που εκπέμπει η χορδή. Συγκεκριμένα, αν η χορδή μίκραινε ως τα 3/4 του αρχικού μήκους της, τότε ακουγόταν η τέταρτη ως προς τον αρχικό τόνο. Αν μίκραινε ως τα 2/3 του αρχικού μήκους της, τότε ακουγόταν η πέμπτη και αν ως το 1/2 του αρχικού μήκους της, τότε ακουγόταν η διαπασών. Επομένως όταν το αρχικό μήκος της χορδής ήταν 12, η τέταρτη ακούγεται όταν η χορδή μικρύνει ως το 9, η Πέμπτη όταν μικρύνει στο 8 και η διαπασών όταν γίνει 6.

Η ανακάλυψη της σχέσης «μήκους χορδής» και «ύψους τόνου» είναι ο πρώτος φυσικός νόμος που βρέθηκε εμπειρικά.

Ο Πυθαγόρας έθετε τα ερωτήματα: «ποιο είναι το αίτιο;» και «ποιο είναι το αποτέλεσμα;» Το αίτιο ήταν οι λόγοι

και το αποτέλεσμα η μουσική αρμονία.

Για τους αριθμούς 6, 8, 9 και 12 έχουν κάποιες αριθμητικές «ιδιαιτερότητες».

• ο 9 είναι ο αριθμητικός μέσος των 6 και 12, δηλαδή 
• ο 8 είναι ο αρμονικός μέσος των 6 και 12, δηλαδή

• 

(αυτό σημαίνει ότι οι χορδές με μήκη 12 και 9, όπως και οι χορδές με μήκη 8 και 6 δίνουν έναν τόνο και την τέταρτη)

 

• 

(αυτό σημαίνει ότι οι χορδές με μήκη 12 και 8, όπως και οι χορδές με μήκη 9 και 6 δίνουν έναν τόνο και την πέμπτη) .

 

Οι αριθμοί 6, 8 και 12 έχουν ιδιαίτερες ιδιότητες όχι μόνο στην αριθμητική και τη μουσική, αλλά και στη γεωμετρία. Για παράδειγμα, ο κύβος έχει 6 έδρες, 8 κορυφές και 12 ακμές. Επειδή έχει βρεθεί μια μουσική αρμονία που σχετίζεται με τους αριθμούς 6, 8 και 12, έτσι ο κύβος για τους πυθαγόρειους θεωρείται «αρμονικό σώμα».

Η σχέση των αριθμών με τη μουσική για τον Πυθαγόρα ήταν απόδειξη πως ο αριθμός παίζει καθοριστικό ρόλο στα πράγματα της καθημερινότητάς μας. Έτσι οι πυθαγόρειοι πίστεψαν πως η ουσία των όντων είναι ο αριθμός και κάθε γνώση μπορεί να αναχθεί σε σχέσεις μεταξύ αριθμών.

 

Τα Αριθμητικά των Πυθαγορείων

Την Αριθμητική όπως την εννοούμε σήμερα, οι αρχαίοι Έλληνες τη διέκριναν:

• στη Λογιστική, δηλαδή το υπολογιστικό μέρος των μαθηματικών
  (υπολογιστικές διαδικασίες ή αλγόριθμους) και
• στα Αριθμητικά, τα οποία ασχολούνται με τη μελέτη των ιδιοτήτων των αριθμών, κυρίως των θετικών ακέραιων. Η εξέλιξη των Αριθμητικών στη σύγχρονη εποχή είναι η Θεωρία αριθμών ή Αριθμοθεωρία.

Με τη Λογιστική ασχολούνταν οι έμποροι και οι δούλοι ενώ με τα Αριθμητικά οι φιλόσοφοι και αυτοί που ανήκαν στις ανώτερες τάξεις.

Ο Πυθαγόρας επηρεασμένος από τον βαβυλωνιακό πολιτισμό πίστευε ότι:

«ο αριθμός είναι η ουσία των όντων και συνεπώς έχει μαγική δύναμη».

Κατά τον πυθαγόρειο Φιλόλαο το καθετί που γνωρίζουμε σχετίζεται με έναν αριθμό, ώστε να μπορούμε να το γνωρίσουμε και να το καταλάβουμε με τη λογική.

«Το Ένα είναι η αρχή του παντός»

Για τους Πυθαγόρειους οι αριθμοί ήταν ορισμένα πλήθη ορισμένων αντικειμένων και τους απεικόνιζαν με «ψήφους» (τελείες). Έναν άρτιο αριθμό τον παρίσταναν με μια σειρά ψήφων, που μπορούσε να χωριστεί σε δύο ισοπληθείς ομάδες.

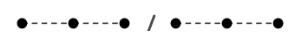
Ένας περιττός αριθμός όμως δεν μπορεί να χωριστεί σε δύο ισοπληθείς ομάδες, γιατί πάντοτε θα περισσεύει μία ψήφος.

Στα Αριθμητικά υπάγεται η θεωρία των παραστατικών αριθμών, όπου υπάρχουν συσχετισμοί μεταξύ των Αριθμητικών και της Γεωμετρίας. Οι Πυθαγόρειοι αντιστοίχιζαν στον αριθμό 1 ένα σημείο, στο 3 τρία σημεία ή ένα τρίγωνο κ.λπ. .

Ετερομήκεις ονόμαζαν τους αριθμούς που μπορούν να γραφούν ως γινόμενο δύο διαδοχικών φυσικών αριθμών.

Στο διπλανό σχήμα ο αριθμός 20 γράφεται 4 · 5

 

Οι αριθμοί 1, 2, 3 και 4 θεωρούνταν ως οι τέσσερις θεμελιώδεις αριθμοί.
Το άθροισμά τους 1+2+3+4=10 λέγεται τετρακτύς

Το 10 είναι η πηγή κάθε δημιουργίας και παριστάνεται με σημεία, των οποίων η διάταξη σχηματίζει ισόπλευρο τρίγωνο, του οποίου κάθε πλευρά έχει τέσσερα σημεία.

 

Οι Πυθαγόρειοι έδιναν στους αριθμούς ιδιότητες μη μαθηματικές ιδιότητες.

Τους περιττούς αριθμούς τους έλεγαν αρσενικούς και τους άρτιους θηλυκούς.

Ο αριθμός 5 = 2+3, που είναι το άθροισμα του πρώτου άρτιου, δηλαδή του 2 και του πρώτου περιττού, δηλαδή του 3 (ο αριθμός 1 δε θεωρήθηκε αριθμός αλλά η αρχή όλων των αριθμών), ήταν το σύμβολο του γάμου.

Οι τετράγωνοι αριθμοί π.χ. 4=2² , 9=3²  κ.λπ. συμβόλιζαν τη δικαιοσύνη (ανταπόδοση των ίσων).

Το 6 την ψυχή, το 7 την αντίληψη και την υγεία, το 8 τον έρωτα και τη φιλία (οι συσχετισμοί αυτοί δεν είναι κατανοητοί).

 

Οι Πυθαγόρειοι ασχολήθηκαν με την έρευνα των τέλειων και των φίλιων αριθμών.

Τέλειος αριθμοί λέγεται ο αριθμός που είναι ίσος με το άθροισμα των γνήσιων διαιρετών του (δηλαδή εξαιρείται από τους διαιρέτες του ο εαυτός του).

Για παράδειγμα ο αριθμός 6 έχει γνήσιους διαιρέτες τους αριθμούς 1, 2 και 3. Επειδή ισχύει 1+2+3 = 6 , ο αριθμός 6 είναι τέλειος. Τέλειοι αριθμοί είναι ακόμα ο 28 και ο 496.

Οι τέλειοι αριθμοί είναι εξαιρετικά σπάνιοι. Ο M. Mersenne (1588-1642) παρατήρησε ότι «οι τέλειοι αριθμοί είναι τόσο σπάνιοι όσο και οι τέλειοι άνθρωποι».

Μέχρι σήμερα κανείς δεν έχει βρει περιττό τέλειο αριθμό, αλλά ούτε έχει αποδειχθεί ότι δεν υπάρχουν περιττοί τέλειοι αριθμοί.

Φίλιοι λέγονται δύο αριθμοί, αν ο καθένας τους είναι ίσος με το άθροισμα των γνήσιων διαιρετών του άλλου, π.χ. οι αριθμοί 220 και 284 είναι φίλιοι.
Το ζευγάρι αυτών των αριθμών έλεγαν ότι αποτελεί σύμβολο φιλίας. Στον Μεσαίωνα οι αριθμοί αυτοί έπαιζαν σπουδαίο ρόλο στη μαγεία, στην αστρολογία και κατασκεύαζαν φυλακτά που είχαν χαραγμένους τους αριθμούς αυτούς.

Το 220 και το 284 δεν είναι οι μόνοι φίλιοι αριθμοί.
Ο Fermat  βρήκε το ζεύγος 17.296, 18.416 , ο Descartes βρήκε το ζεύγος 9.363.584, 9.437.056 και ο Euler βρήκε 62 τέτοια ζεύγη φίλιων αριθμών.

Τα ζεύγη των φίλιων αριθμών μέχρι το 10.000 είναι:
(220, 284),   (1184, 1210) ,   (2620, 2924),   (502, 5564)  και  (6232, 6368).

 

Γεωμετρία

Ο Πυθαγόρας συσχέτιζε τη Γεωμετρία με τους αριθμούς. Το σημείο το αντιστοίχιζαν στον αριθμό 1, την ευθεία (που ορίζεται από δύο σημεία) την αντιστοίχιζαν στον αριθμό 2, το επίπεδο (που ορίζεται από τρία σημεία) το αντιστοίχιζαν στον αριθμό 3 και τον χώρο στον αριθμό 4.

Η πιο γνωστή γεωμετρική ανακάλυψη του Πυθαγόρα είναι το ομώνυμο θεώρημα, σύμφωνα με το οποίο:

«σε κάθε ορθογώνιο τρίγωνο το τετράγωνο της υποτείνουσάς του είναι ίσο με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του».

Η διατύπωση του θεωρήματος και η απόδειξή του αναφέρεται στο πρώτο βιβλίο των Στοιχείων του Ευκλείδη. Επίσης λέγεται ότι μετά από αυτήν την ανακάλυψή του θυσίασε προς τους θεούς εκατό βόδια (εκατόμβη), γι’ αυτό και το θεώρημα αυτό ονομάσθηκε «Εκατόμβη» ή «Θεώρημα εκατόμβης».

Μια σημαντική ανακάλυψη των Πυθαγορείων ήταν η μέθοδος εύρεσης των «πυθαγόρειων τριάδων».

(Τρεις αριθμοί (α , β , γ) αποτελούν πυθαγόρεια τριάδα αν ικανοποιούν τη σχέση  α²+β²=γ²)

Σύμφωνα με τον Πρόκλο, ο Πυθαγόρας ανακάλυψε τις πυθαγόρειες τριάδες της μορφής

 

όπου ν περιττός αριθμός μεγαλύτερος του 1.

Οι Πυθαγόρειοι είχαν μελετήσει τις παράλληλες ευθείες και είχαν αποδείξει ότι το άθροισμα των γωνιών τριγώνου είναι ίσο με 180⁰ .

Επίσης θεωρείται ότι γνώριζαν τα πέντε κανονικά πολύεδρα τετράεδρο, κύβος, οκτάεδρο, δωδεκάεδρο και εικοσάεδρο, τα οποία μεταγενέστερα ονομάστηκαν Πλατωνικά Στερεά. Οι Πυθαγόρειοι είχαν ασχοληθεί με τη μελέτη του τετράεδρου, του κύβου και του δωδεκάεδρου. Ο Θεαίτητος (μαθητής του Πλάτωνα) ασχολήθηκε με τη μελέτη του οκταέδρου και του εικοσαέδρου.

Ασύμμετρα ευθύγραμμα τμήματα και ασύμμετροι (άρρητοι) αριθμοί

Μία από τις σημαντικότερες ανακαλύψεις των Πυθαγορείων είναι η ανακάλυψη των ασύμμετρων (άρρητων) αριθμών, που προέκυψε από τη μελέτη γεωμετρικών εννοιών.

Οι ρητοί (ή σύμμετροι) αριθμοί είναι όλοι οι αριθμοί που μπορούν να γραφούν με τη του μορφή όπου μ, ν ακέραιοι αριθμοί και ν ≠ 0. Οι αριθμοί που δεν μπορούν να γραφούν ως πηλίκα δύο ακεραίων αριθμών, δηλαδή δεν είναι ρητοί, λέγονται άρρητοι (ή ασύμμετροι) αριθμοί.

Ποια ευθύγραμμα τμήματα λέγονται σύμμετρα;

«Θεωρούμε δύο μη μηδενικά ευθύγραμμα τμήματα ΑΒ και ΓΔ. Αν υπάρχει ευθύγραμμο τμήμα ΜΝ και φυσικοί αριθμοί κ, λ τέτοιοι ώστε να ισχύει:  ΑΒ = κ ΜΝ και ΓΔ = λ ΜΝ, τα ευθύγραμμα τμήματα ΑΒ και ΓΔ λέγονται σύμμετρα και το ευθύγραμμο τμήμα ΜΝ λέγεται κοινό μέτρο των ΑΒ και ΓΔ».

Άρα υπάρχει θετικός ρητός αριθμός    

τέτοιος ώστε να ισχύει: ΑΒ = ρ ·ΓΔ .

Ο αριθμός ρ λέγεται λόγος του ΑΒ προς το ΓΔ και γράφεται:  

«Ασύμμετρα λέγονται δύο ευθύγραμμα τμήματα που δεν είναι σύμμετρα, δηλαδή δεν έχουν κοινό μέτρο. Λέμε ακόμα ότι ο λόγος τους είναι άρρητος αριθμός».

Οι Πυθαγόρειοι ανακάλυψαν ότι η πλευρά και η υποτείνουσα ενός ορθογωνίου και ισοσκελούς τριγώνου είναι ασύμμετρα ευθύγραμμα τμήματα».

Πράγματι, το τρίγωνο ΑΒΓ του διπλανού σχήματος είναι ορθογώνιο και ισοσκελές. Σύμφωνα με το Πυθαγόρειο θεώρημα ισχύει:

Αν τα ευθύγραμμα τμήματα ΒΓ και ΑΒ ήταν σύμμετρα, ο λόγος τους θα ήταν ρητός αριθμός. Όμως δεν υπάρχει ρητός αριθμός, του οποίου το τετράγωνο είναι ίσο με 2, οπότε τα ευθύγραμμα τμήματα ΒΓ και ΑΒ δεν είναι σύμμετρα, αφού ο λόγος τους δεν είναι με ρητός αριθμός. Ο λόγος τους είναι άρρητος αριθμός, λέγεται τετραγωνική ρίζα του 2 και συμβολίζεται με √2.

Οι αρχαίοι Έλληνες πίστευαν ότι πάντοτε δύο ευθύγραμμα τμήματα είναι σύμμετρα, δηλαδή ο λόγος τους είναι ρητός αριθμός. Με την ανακάλυψη των άρρητων αριθμών ανατράπηκαν θεμελιώδεις αντιλήψεις των Πυθαγορείων για τον κόσμο και τη φύση.

Η βάση όλης της κοσμοθεωρίας τους ήταν «η ουσία κάθε όντος μπορεί να αναχθεί σε φυσικούς αριθμούς».
Ο νεοπυθαγόρειος Φιλόλαος έγραψε: «Πραγματικά το καθετί που γνωρίζουμε έχει ένα αριθμό (φυσικό). Αλλιώς είναι αδύνατο να το γνωρίσουμε και να το καταλάβουμε με τη λογική. Το ένα είναι η αρχή του παντός».

Υπάρχουν διάφοροι θρύλοι σχετικοί με την ανακάλυψη των άρρητων αριθμών. Σύμφωνα με έναν από τους θρύλους αυτούς, ο Ίππασος ο Μεταπόντιος ήταν ο άνθρωπος που αποκάλυψε την ανακάλυψη των άρρητων ααριθμών. Όμως η αποκάλυψη αυτή παραβίαζε τον νόμο των Πυθαγορείων, ότι έπρεπε να μένουν οι ανακαλύψεις τους άγραφα μυστικά. Έτσι οι θεοί για να τον τιμωρήσουν για την αποκάλυψη του μυστικού τον έπνιξαν.

Κατά έναν άλλο θρύλο ο Ίππασος ανακάλυψε του άρρητους αριθμούς, όταν μαζί με άλλους Πυθαγόρειους ταξίδευε με πλοίο. Αυτοί έπνιξαν τον Ίππασο ώστε να μη γίνει γνωστή η ανακάλυψη. Υπάρχει όμως και ένας άλλος θρύλος, σύμφωνα με τον οποίο έγινε θυσία για να τιμηθεί η ανακάλυψη.

 

Αστρονομία

Ο Πυθαγόρας θεώρησε ότι το σύμπαν δημιουργήθηκε με αλλεπάλληλες ομόκεντρες σφαίρες. Αυτές ήταν:

• η αρχική εξωτερική σφαίρα
• μία σφαίρα με όλους τους απλανείς (την οποία θεωρούσαν ως ένα ουράνιο σώμα)
• από μία σφαίρα για κάθε έναν από τους πέντε πλανήτες (Κρόνο, Δία, Άρη, Αφροδίτη και Ερμή) και
• από μία σφαίρα για τον Ήλιο, τη Γη και τη Σελήνη.

Επομένως κατά τους Πυθαγόρειους υπήρχαν συνολικά 9 ουράνια σώματα.

Αυτά περιστρέφονταν γύρω από ένα κοινό κέντρο, που το ονόμαζαν «κεντρικόν πῦρ» ή «Ἑστία τοῦ παντός», που δεν το ταύτισε με τον Ήλιο. Εκεί κατοικούσε ο Δίας, ο κύριος του σύμπαντος.

Ο αριθμός 9 όμως δεν ήταν τόσο σημαντικός όσο ο αριθμός 10. Για τον λόγο αυτόν δέχτηκαν την ύπαρξη 10^ου ουράνιου σώματος μη ορατού από τη Γη, που ήταν η «Ἀντίχϑων».

Για να δικαιολογήσουν ότι η Ἀντίχϑων δεν είναι ορατή από τη Γη, διατύπωσαν τη θεωρία ότι: «η Γη στρέφεται κατά τέτοιον τρόπο, ώστε το ακατοίκητο μέρος της να είναι πάντα στραμμένο προς την Ἑστία τοῦ παντός και η Ἀντίχϑων είναι τοποθετημένη μεταξύ Γης και Ἑστίας».

Ο Πυθαγόρας ήταν ο πρώτος φιλόσοφος που συνέδεσε την Αστρονομία με τη Μουσική. Πρώτος ο Αριστοτέλης στο βιβλίο του «Περί Ουρανού» μιλάει για τη θεωρία των Πυθαγορείων ότι τα ουράνια σώματα με τις κινήσεις τους στον χώρο παράγουν μουσική. Όπως τα γήινα σώματα μετακινούμενα στον αέρα προκαλούν δονήσεις, έτσι και τα ουράνια σώματα κινούμενα μέσα στον αιθέρα παράγουν ήχους. Αυτή η ουράνια μουσική, η «αρμονία των σφαιρών», δε γίνεται αισθητή από τους ανθρώπους γιατί είναι συνεχής και επομένως οι άνθρωποι την έχουν συνηθίσει.

Η NASA στα τέλη της δεκαετίας του 1970 με το πρόγραμμα Voyager εκτόξευσε δύο διαστημόπλοια, το Voyager 1 και το Voyager 2. Αυτά κατέγραψαν τα ηλεκτρομαγνητικά κύματα που δημιουργούνται στο διάστημα και με έναν πομπό τα έστειλαν στη Γη.

Η NASA τα μετέτρεψε σε ήχους και το 1992 κυκλοφόρησε δίσκο με τους ήχους αυτούς υπό τον τίτλο «Symphonies Of The Planets – NASA Voyager Recordings».

Έτσι θα μπορούσε να πει κάποιος, με μια ρομαντική προσέγγιση, ότι ήταν μια «επαλήθευση» της θεωρίας του Πυθαγόρα σχεδόν μετά από 2.500 χρόνια.

 

Επίλογος  

Ο Πυθαγόρας δεν άφησε κανένα γραπτό κείμενο. Η διδασκαλία του έγινε γνωστή και διαδόθηκε μέσα από τα γραπτά κείμενα των μαθητών του.

Υπήρξε μεγάλος μαθηματικός, ο οποίος πρέσβευε ότι τα Μαθηματικά είναι ο δρόμος για την απελευθέρωση της ψυχής.

Ήταν ο πρώτος άνθρωπος που χρησιμοποίησε (για τον εαυτό του) τη λέξη «φιλόσοφος», για να δηλώσει την αγάπη του για τη σοφία και ήταν ιδρυτής ενός φιλοσοφικού κινήματος του Πυθαγορισμού.

Υπήρξε θεωρητικός της Μουσικής, αφού ήταν ο πρώτος άνθρωπος που ανακάλυψε τα μουσικά διαστήματα με τη μελέτη μιας χορδής (το μονόχορδο).

Ήταν ο πρώτος που ονόμασε το σύμπαν «κόσμο» (στολίδι), λόγω της τελειότητάς του και της ομορφιάς του. Καθόρισε την τάξη των ουράνιων σωμάτων και ήταν επίσης ο πρώτος φιλόσοφος που συνδύασε την Αστρονομία με τη Μουσική.

 

Πηγές

1. Βλάμος Παναγιώτης, Δρούτσας Παναγιώτης, Πρέσβης Γεώργιος, Ρεκούμης Κωνσταντίνος, (2016). Μαθηματικά Β’Γυμνασίου. Έκδοση Ι.Τ.Υ.Ε. «ΔΙΟΦΑΝΤΟΣ».
2. Αργυρόπουλος Ηλίας, Βλάμος Παναγιώτης, Κατσούλης Γεώργιος, Μαρκάτης Στυλιανός, Σιδέρης Πολυχρόνης (2015). ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Α΄και Β΄ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ. Έκδοση Ι.Τ.Υ.Ε. «ΔΙΟΦΑΝΤΟΣ».
3. Αραμπατζής Θεόδωρος, Γαβρόγλου Κώστας, Διαλέτης Δημήτρης, Χριστιανίδης Γιάννης, Κανδεράκης Νίκος, Βερνίκος Στέλιος (1999). Ιστορία των επιστημών και της τεχνολογίας Γ΄ Λυκείου. Έκδοση Ο.Ε.Δ.Β. .
4. ΙΑΜΒΛΙΧΟΣ Περί Του Πυθαγορικού Βίου Τόμος Α’-Β’. Ειδική έκδοση για την εφημερίδα ΤΟ ΒΗΜΑ, εκδόσεις ΖΗΤΡΟΣ.
5. Lucas N. H. Bunt, Phillip S. Jones, Jack D. Bedient (1981). Οι Ιστορικές Ρίζες Των Στοιχειωδών Μαθηματικών. Επιστημονικές και Τεχνικές Εκδόσεις Γ.Α. Πνευματικός. Τίτλος πρωτοτύπου: The Istorical Roots of ElementaryMathematics (Prentice-Hall, Inc., Englewood Cliffs, New Jersey). Μετάφραση: Άννα Φερεντίνου-Νικολακοπούλου.
6. Συγγραφική ομάδα «Καλώς Κείμενα» (Ευάγγελος Χεκίμογλου, Ευφροσύνη Ρούπα, Αικατερίνη Αναστασίου, Ναυσικά Στεργίου, Πόπη Μητσοπούλου) (2017). 70 ΕΠΙΣΤΗΜΟΝΕΣ ΠΟΥ ΑΛΛΑΞΑΝ ΤΟΝ ΚΟΣΜΟ. Ειδική έκδοση για την εφημερίδα ΤΑ ΝΕΑ, εκδόσεις ΑΛΤΕΡ ΕΓΚΟ Α.Ε. .

 

Ηλ. Ταχ.: [email protected]

 

Τάσσος Κυρίκος

Μαθηματικός